Internal clearance
This is generally referred to as radial play although it also incorporates axial play as well because it is actually the amount of space between the rolling elements of the bearing, namely inner ring, outer ring and balls.
 |
|
 |
| |
|
|
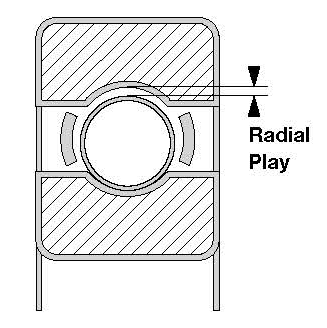
| Radial Play - is clearance perpendicular to the axis of the bearing and better described as the movement available to the outer ring when inner is fixed. This can be more accurately defined as follows: average diameter outer ring raceway minus average diameter of inner ring minus x2 ball diameter. |
|
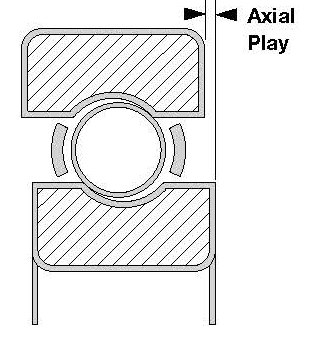
Axial Play - is the opposite of radial play as it is the movement of the rings relative to each other along the axis of the bearing. The amount of axial play is controlled by the bearing raceway curvature but as a general rule is around x10 the value of radial play. |
Radial play is a major consideration when selecting a bearing. Prior to fitting a bearing has an ‘initial’ amount of play and after being mounted it has a ‘residual’ radial play (sometimes referred to as operational radial play as it is what is remaining). When a shaft is supported between bearings then consideration needs to be given to the alignment of the bearings as misalignment reduces radial play, therefore it is important that selection accounts for this. There should always be some ‘residual’ radial play after fitting as this extends bearing life by avoiding skidding and reducing axial play.
There are a number of things that can change radial play during fitting. A tight shaft, larger than the inner ring, will expand the inner ring and this can reduce radial play up to 80% of the interference fit. The same thing happens if the outer ring is larger than the housing diameter, the ring is effectively compressed and reduces radial play in the same way. If there was a temperature difference seen between the shaft and the housing then thermal expansion either on the inner or outer ring, would lead to a reduction in radial play. This may be calculated as opposite:
Chrome Steel - 0.0000125 x (inner ring temp - outer ring temp °C) x outer ring raceway diameter in mm.
440 Stainless Steel - 0.0000103 x (inner ring temp - outer ring temp °C) x outer ring raceway diameter in mm.
The outer ring raceway diameter is roughly calculated as: 0.2 x (d + 4D) where d is the bore in mm and D is the outer diameter in mm.
Another factor to consider relating to thermal expansion is the material that is used for the shaft and housing. For example, a housing material with a higher coefficient of expansion than the bearing material could under certain conditions ‘squeeze’ the bearing outer ring and reduce radial play.